Trying to find a solution to a puzzle using C#. This article uses a lot of LINQ. It embeds FlowSharp so you can watch the algorithm go through the process of finding a solution, implements three different algorithms so you can peruse the pros and cons of each: Iterative, Recursive using yield, and Recursive with callback.
Contents
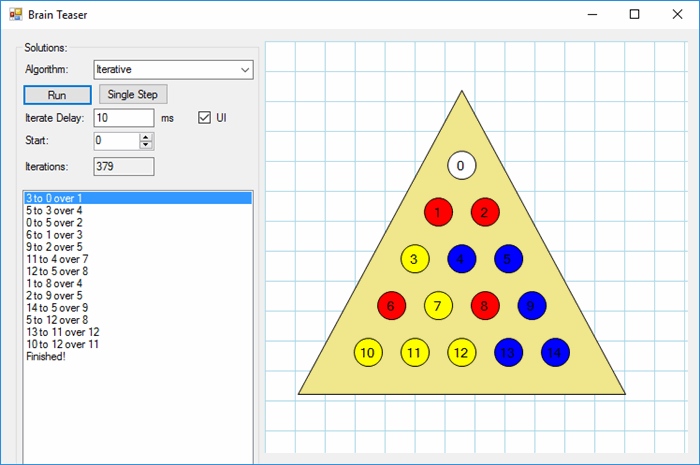
We have these brain teaser puzzles at work:

We've probably all played them -- the idea being you start with one empty hole, the rest are filled with pegs, and each move consists of hopping a peg to an empty location, thus removing the peg you just hopped. The goal is to remain with just one peg left.
For a roomful of programmers, no one (including me!) so far has been able to solve the puzzle. Watching one of my coworkers futility go through various failed iterations, I had the obvious thought -- write a program to find solutions to the puzzle! The second obvious thought was, someone must have done this! Well, turns out, not really.
OK, so while there are several solutions, I actually didn't find one in C#, and even if I had, there is a certain pleasure in writing something like this oneself, even if it's been done before. And of course, one can challenge oneself to write the code as elegantly and efficiently as possible, etc. And more to the point, none of the algorithms presented:
- had a snazzy UI so you could watch the algorithm processing.
- implemented iteration and recursion alternatives.
Ah, opportunity!
 And as is apt to occur, I went way overboard.
And as is apt to occur, I went way overboard.
So the solution I present here:
- Has a funky extension method which may or may not make the code more readable.
- Uses a lot of Linq.
- Embeds FlowSharp so you can watch the algorithm go through the process of finding a solution (why re-invent the wheel?)
- Let's you single step through the solution and watch each step so you can memorize the solution and impress your friends!
- As with the actual cheap game, there are 3 different colored pegs -- yellow, blue, and red -- which the UI implements, randomly assigned when you start the demo.
- Implements three different algorithms so you can peruse the pros and cons of each:
- Iterative -- the search stack is handled as handled as an actual
Stack object. - Recursive using
yield -- the search stack is an artifact of recursion. - Recursive with callback -- again the search stack is an artifact of recursion.
- Was fun to write!
Regarding the source code:
- The SLN file is found in the BrainTeaser folder.
- The actual demo app is found in the Demo folder.
- If you want to play around with recursive yields, there's a YieldTest folder with a simple demo (shown later in the article.)
- The Libs folder contains all the dependencies that FlowSharp uses, so you do not have to download and build that project.
A lot of the work is done up front by setting up collections that have pre-determined all the possible "hops" from one "cell" to another. The algorithm only needs to determine which of these "hops" is legal for the current board configuration.
I decided to borrow from Ruby to create an extension method that iterates on an integer with an optional starting offset:
public static void ForEach(this int i, Action<int> action, int startIdx = 0)
{
for (int n = startIdx; n < i + startIdx; n++) action(n);
}
You'll see that used next.
I also use this extension method to convert a color to an HTML color of the form #RRGGBB:
public static string ToHtmlColor(this Color c, char prefix = '#')
{
return prefix + c.R.ToString("X2") + c.G.ToString("X2") + c.B.ToString("X2");
}
The basic data structures are the Row and Cell.
The board consists of an array of rows:
protected Row[] rows;
which consist of an array of cells:
public class Row
{
public Cell[] Cells { get; protected set; }
public Row(int numCells)
{
Cells = new Cell[numCells];
numCells.ForEach(n => Cells[n] = new Cell());
}
}
There's that first extension method!
Initialization of the game board embeds the rule that the number of cells is equal to the 1-base index of the row number:
protected void InitializeRowsAndColumns(int numRows)
{
rows = new Row[numRows];
numRows.ForEach(n => rows[n] = new Row(n + 1));
}
There's that first extension method again!
A cell consists of its state (empty or has a peg) and an initial random seed of the peg color:
public class Cell
{
public Color Color { get; set; }
public bool HasPeg { get { return state; } set { state = value; } }
public bool IsEmpty { get { return !state; } }
protected bool state;
private static Random rnd = new Random(DateTime.Now.Second);
private static Color[] colors = { Color.Red, Color.Blue, Color.Yellow };
public Cell()
{
Color = colors[rnd.Next(colors.Length)];
}
}
Note the HasPeg and IsEmpty properties, which improve the code readability in other methods, rather than exposing state. Also note that the cell contains a static Random instance and the collection of possible peg colors.
Except for initialization, the algorithm to solve the puzzle works with integer indices of the cells, rather than their row/column location. Among other things, this simplifies how possible hops are determined, as well as updating the UI. It's a lot easier (and more performant) if you don't constantly have to look up a cell state by it's row/column location. So internally, the board maintains a flat view of all the cells:
protected List<Cell> flatView;
Initialization of the flat view is straightforward:
protected void InitializeFlatView()
{
flatView = new List<Cell>();
rows.ForEach(r => r.Cells.ForEach(c => flatView.Add(c)));
}
This illustrates an important point: there are often two or more ways to model a structure, and depending on what you're doing, it's easier to work with one model vs. another. We see this next, where initializing all the hops is more readable if we work with the row/column model.
A cell location (as a row/column) mapped to its index in the flat view (above) is useful for initialization. The mapping is done with a dictionary:
protected Dictionary<Location, int> cellToIndexMap;
but when we use a structure as the dictionary key, a simple way (without writing comparison operators) is to represent the structure as a C# struct rather than a class:
public struct Location
{
public int Row { get; set; }
public int Column { get; set; }
public Location(int row, int column)
{
Row = row;
Column = column;
}
}
Why? By using a struct, the key is compared by value as opposed to by reference.
We then initialize map:
protected void InitializeCellToIndexMap()
{
cellToIndexMap = new Dictionary<Location, int>();
int n = 0;
rows.ForEachWithIndex((r, ridx) => r.Cells.ForEachWithIndex((c, cidx) => cellToIndexMap[new Location(ridx, cidx)] = n++));
}
This is used next.
The workhorse of the algorithm depends on initializing a structure that contains all possible hops (validity of the hop is checked later.) This takes advantage of the cell location to index map that we created earlier. Here we introduce the Hop class:
public class Hop
{
public int FromCellIndex { get; protected set; }
public int ToCellIndex { get; protected set; }
public int HoppedCellIndex { get; protected set; }
public Color FromCellColor { get; set; }
public Color HoppedCellColor { get; set; }
public Color ToCellColor { get; set; }
public Hop(int from, int to, int hopped)
{
FromCellIndex = from;
ToCellIndex = to;
HoppedCellIndex = hopped;
}
public Hop Clone()
{
Hop hop = new Hop(FromCellIndex, ToCellIndex, HoppedCellIndex);
return hop;
}
public override string ToString()
{
string ret = "Finished!";
if (FromCellIndex != -1)
{
ret = FromCellIndex.ToString() + " to " + ToCellIndex.ToString() + " over " + HoppedCellIndex.ToString();
}
return ret;
}
}
Notice a few things about the Hop class:
- A hop knows its from, to, and cell hopped over indices.
- A hop preserves the state of the peg colors involved in the hop. We'll see later that these colors are assigned when a hop is made based on the current game board state.
- Notice the
Clone method. In the board's model, there is only one instance of each possible hop. However, because a hop preserves color state information, we need a cloned instance for the reason that the comment states. - The
ToString() method gives us an easy way to display the solution in a ListBox of hops.
 The issue of preserving color was actually the hardest bug to solve. It took me quite a while to realize that the Hop instance was being re-used for multiple iterations, thus overwriting the colors of a previous iteration!
The issue of preserving color was actually the hardest bug to solve. It took me quite a while to realize that the Hop instance was being re-used for multiple iterations, thus overwriting the colors of a previous iteration!
Initializing all the possible hops populates the List<Hop> allHops structure:
protected void InitializeAllHops()
{
allHops = new List<Hop>();
rows.ForEachWithIndex((r, ridx) =>
{
r.Cells.ForEachWithIndex((c, cidx) =>
{
AddHorizontalHop(r, ridx, cidx);
if (rows.Length > ridx + 2)
{
AddDiagonalLeftHop(r, ridx, cidx);
AddDiagonalRightHop(r, ridx, cidx);
}
});
});
}
protected void AddHorizontalHop(Row r, int ridx, int cidx)
{
if (r.Cells.Length > cidx + 2)
{
int fromIdx = GetIndex(ridx, cidx);
int toIdx = GetIndex(ridx, cidx + 2);
int hopIdx = GetIndex(ridx, cidx + 1);
AddHop(fromIdx, toIdx, hopIdx);
}
}
protected void AddDiagonalLeftHop(Row r, int ridx, int cidx)
{
int fromIdx = GetIndex(ridx, cidx);
int toIdx = GetIndex(ridx + 2, cidx);
int hopIdx = GetIndex(ridx + 1, cidx);
AddHop(fromIdx, toIdx, hopIdx);
}
protected void AddDiagonalRightHop(Row r, int ridx, int cidx)
{
int fromIdx = GetIndex(ridx, cidx);
int toIdx = GetIndex(ridx + 2, cidx + 2);
int hopIdx = GetIndex(ridx + 1, cidx + 1);
AddHop(fromIdx, toIdx, hopIdx);
}
And because hops can be performed "forward" and "backwards":
protected void AddHop(int fromIdx, int toIdx, int hopIdx)
{
allHops.Add(new Hop(fromIdx, toIdx, hopIdx));
allHops.Add(new Hop(toIdx, fromIdx, hopIdx));
}
The method GetIndex asserts that the index can be obtained for the row/column by verifying the existence of the map key:
public int GetIndex(int row, int col)
{
int idx;
bool found = cellToIndexMap.TryGetValue(new Location(row, col), out idx);
Assert.That(found, string.Format("Location at {0}, {1} does not exist.", row, col));
return idx;
}
This is a fun Linq expression that joins the flat view index with the fromCellIndex of all possible hops and filtering the return for only "from" cells where the "to" cell is empty and the cell being hopped over has a peg:
public List<Hop> GetAllowedHops()
{
var allowedHops = Enumerable.Range(0, flatView.Count()).
Where(n => flatView[n].HasPeg).
Join(allHops, pegIdx => pegIdx, hop => hop.FromCellIndex, (pegIdx, hop) => hop).
Where(hop => flatView[hop.ToCellIndex].IsEmpty && flatView[hop.HoppedCellIndex].HasPeg).
Select(hop => hop.Clone()).ToList();
return allowedHops;
}
Lastly, the Board class provides the methods for performing a hop, or undoing a hop. Undoing a hop is necessary when unwinding the collection of hops for a failed solution, which we'll look at in the algorithm section.
public void HopPeg(Hop hop)
{
Assert.That(flatView[hop.FromCellIndex].HasPeg, "Expected from cell to be have a peg.");
Assert.That(flatView[hop.ToCellIndex].IsEmpty, "Expected to cell to be empty.");
Assert.That(flatView[hop.HoppedCellIndex].HasPeg, "Expected to cell have a peg.");
flatView[hop.FromCellIndex].HasPeg = false;
flatView[hop.HoppedCellIndex].HasPeg = false;
flatView[hop.ToCellIndex].HasPeg = true;
hop.FromCellColor = flatView[hop.FromCellIndex].Color;
hop.HoppedCellColor = flatView[hop.HoppedCellIndex].Color;
hop.ToCellColor = flatView[hop.ToCellIndex].Color;
flatView[hop.ToCellIndex].Color = hop.FromCellColor;
DoHop.Fire(this, new CellChangeEventArgs() { Hop = hop, State = true });
}
public void UndoHopPeg(Hop hop)
{
Assert.That(flatView[hop.FromCellIndex].IsEmpty, "Expected from cell to be empty.");
Assert.That(flatView[hop.ToCellIndex].HasPeg, "Expected to cell to have a peg.");
Assert.That(flatView[hop.HoppedCellIndex].IsEmpty, "Expected to cell to be empty.");
flatView[hop.FromCellIndex].HasPeg = true;
flatView[hop.HoppedCellIndex].HasPeg = true;
flatView[hop.ToCellIndex].HasPeg = false;
flatView[hop.FromCellIndex].Color = hop.FromCellColor;
flatView[hop.HoppedCellIndex].Color = hop.HoppedCellColor;
flatView[hop.ToCellIndex].Color = hop.ToCellColor;
UndoHop.Fire(this, new CellChangeEventArgs() { Hop = hop, State = false });
}
Notice that we do some more assertions here, in case the algorithm asked the board to perform an illegal operation. Also notice that we're managing the peg color here, preserving the original color of the peg being hopped over. Lastly, a couple events fire that are wired up by the UI:
public event EventHandler<CellChangeEventArgs> DoHop;
public event EventHandler<CellChangeEventArgs> UndoHop;
We'll look at how the UI uses these events later on.
As other implementations have stated, the algorithm is a Depth First Search (DSF) process. From the link:
"Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. One starts at the root (selecting some arbitrary node as the root in the case of a graph) and explores as far as possible along each branch before backtracking."
In our case, the "root" is all possible hops with just one empty cell. After choosing a hop, all new allowable hops are determined, and the first one is chosen. This process repeats until the puzzle is solved or no further hops can be made. If no further hops can be made, the algorithm unwinds one level and chooses the next hop of allowable hops. If there are no more allowable hops, the algorithm unwinds again. This process is repeated until it gets back to the root's allowable hops. If no solution has been found at that point, the algorithm exits with "no solution found." (Hint -- all the possible starting positions are solvable.)
The following data structures are used.
This is a class that manages all allowable hops for a particular level (board state) and sequencing through that list:
public class HopOptions
{
protected List<Hop> hops;
protected int hopIdx;
public Hop CurrrentHop { get { return hops[hopIdx]; } }
public HopOptions(List<Hop> hops)
{
this.hops = hops;
hopIdx = 0;
}
public bool NextOptionIndex()
{
return ++hopIdx < hops.Count;
}
}
Note that when all the hop options have been exercised, NextOptionIndex returns false, indicating that the stack needs to be unwound.
The hop stack:
public Stack<HopOptions> HopStack { get; protected set; }
maintains the current state of the search algorithm, as a stack. When a hop is made, the hop options for the new board state are pushed onto this stack. When all the possible hops at this level have been exercised, the stack is popped.
The undo stack:
public Stack<Hop> UndoStack { get; protected set; }
is a different representation of the HopStack. The UndoStack tracks the current hop that has been taken. The undo stack could be determined from the HopStack and its current index, so this model is a convenience -- it represents the current path through the HopStack.
You might surmise at this point, since I'm utilizing actual Stack collections, that the algorithm is iterative rather than recursive. A recursive algorithm would utilize the actual program stack for maintaining state. The reason for this is so that we can easily implement a "single step" behavior. A recursive algorithm is not amenable to single stepping through each permutation because it would have to exit all recursion levels and then re-enter them magically to continue with the next step.
This is definitely a possibility. For example, this code:
static void Main(string[] args)
{
YieldTest(0).ForEach(n => Console.WriteLine(n));
}
static IEnumerable<int> YieldTest(int n)
{
yield return n;
if (++n < 5)
{
foreach (int q in YieldTest(n))
{
yield return q;
}
}
}
prints "0 1 2 3 4" and demonstrates how each iteration can be "stepped" by iterating through the enumerator.
A callback for each recursive call would allow the handler to suspend and wait for user input stepper, and unlike the yield operator, has the advantage of being able to return a "cancel" flag.
Because this is one of those "let's have fun" articles, I'll show you how iteration, recursion with yield, and recursion with a step-and-continue callback works.
The iterative algorithm is actually the easiest to implement when dealing with the single step option. It implements the Run method.
public override void Run()
{
while (board.RemainingPegs > 1 && Step())
{
Hop hop = PushHop();
}
Solved = board.RemainingPegs == 1;
}
which does little more than single step through each iteration, pushing state information as it goes along.
Because we are maintaining our own stack (as opposed to a recursive algorithm that maintains the stack as local variables on the program stack), we need to push our current state onto our two stack model representations (the HopStack and the UndoStack):
public override Hop PushHop()
{
Hop hop = HopStack.Peek().CurrrentHop;
board.HopPeg(hop);
UndoStack.Push(hop);
return hop;
}
The Step method is where the iteration is implemented, in the sense that it attempts each possible hop, and when no further hops are possible, the stack is unwound.
public override bool Step()
{
bool next = true;
List<Hop> allowedHops = board.GetAllowedHops();
if (allowedHops.Count == 0)
{
next = Unwind();
}
else
{
HopOptions hopOptions = new HopOptions(allowedHops);
HopStack.Push(hopOptions);
}
return next;
}
When the algorithm cannot move forward anymore, the stacks are unwound until there are more forward iterations possible:
protected bool Unwind()
{
bool more = false;
while (!more && HopStack.Count > 0)
{
Hop undoHop = UndoStack.Pop();
board.UndoHopPeg(undoHop);
more = HopStack.Peek().NextOptionIndex();
if (!more)
{
HopStack.Pop();
}
}
return more;
}
The recursive yield algorithm is much simpler!
public override void Run()
{
foreach(Hop hop in Step(new HopOptions(board.GetAllowedHops())))
{
board.HopPeg(hop);
Solved = board.RemainingPegs == 1;
if (Solved)
{
break;
}
}
}
The neat thing here is that the stepper method Step returns an IEnumerable<Hop>, so all the Run method has to do is iterate through the enumeration until a solution is found. Note the comment.
protected IEnumerable<Hop> Step(HopOptions hopOptions)
{
while (hopOptions.OptionAvailable)
{
Hop hop = hopOptions.CurrrentHop;
UndoStack.Push(hop);
yield return hop;
List<Hop> allowedHops = board.GetAllowedHops();
foreach (Hop nextHop in Step(new HopOptions(allowedHops)))
{
yield return nextHop;
}
UndoStack.Pop();
board.UndoHopPeg(hop);
hopOptions.NextOptionIndex();
}
}
The stepper, because it's implemented as a recursive algorithm, doesn't need to maintain a separate stack -- the recursion passing in the HopOptions hopOptions lets the program stack implement what, in the iterative algorithm, was handled by the Stack<HopOptions> HopStack. Note that we are still implementing the UndoStack push/pop, as this is a separate model for the convenience of the UI.
As the comment earlier mentioned, the neat thing about the yield operator is that it flattens the recursion -- the code looks like recursion, but it actually ends up implementing iteration. Read more:
This algorithm replaces the yield with a callback for updating the game board at every iteration:
protected bool Step(HopOptions hopOptions, Func<Hop, bool> callback)
{
while (hopOptions.OptionAvailable)
{
Hop hop = hopOptions.CurrrentHop;
UndoStack.Push(hop);
if (callback(hop))
{
return false;
}
List<Hop> allowedHops = board.GetAllowedHops();
bool cont = Step(new HopOptions(allowedHops), Callback);
if (!cont)
{
return false;
}
UndoStack.Pop();
board.UndoHopPeg(hop);
hopOptions.NextOptionIndex();
}
return true;
}
The inner for loop that the recursive yield algorithm used is also gone as it's now unnecessary. Note however that we have to provide a mechanism for unraveling the recursion when the algorithm is solved. (This is slight confusing, because the callback returns true if the algorithm is solved, but the stepper returns false if it's supposed to abort.
Running the solver is a simple matter of:
public override void Run()
{
Step(new HopOptions(board.GetAllowedHops()), Callback);
}
The callback is the critical piece, as it returns true if the puzzle has been solved:
protected bool Callback(Hop hop)
{
++Iterations;
board.HopPeg(hop);
Solved = board.RemainingPegs == 1;
return Solved;
}
 Note that at this point, I added an iteration counter to all the algorithms.
Note that at this point, I added an iteration counter to all the algorithms.
So far, the iterative and recursive yield approach have both had the advantage that single stepping easily works on the application thread -- both approaches "return control" to the UI, which (as we will see later) when single stepping, lets the single step button click continue the iteration. This is not the case with a non-yielding, or "step and continue", as I call it, recursion. In order to suspend the recursive algorithm, we have to "gate" the continuation so that the algorithm suspends operation until the user clicks on the single step button. A cheap and dirty approach is to call Application.DoEvents() and spin until a flag is set indicating that the algorithm can continue. This is what I consider a beginner's approach to the problem. A better approach is to use a semaphore to gate the continuation, and to execute the algorithm on a separate thread. This is the approach that I took.
First, we have the semaphore and its initialization:
protected Semaphore hopSemaphore;
public RecursiveStepAndContinueAlgorithm(Board board) : base(board)
{
hopSemaphore = new Semaphore(0, 1);
}
To initialize the stepper, we start a task and wait for the semaphore to be released:
public override void StartStepper()
{
Task.Factory.StartNew(() =>
{
hopSemaphore.WaitOne();
Step(new HopOptions(board.GetAllowedHops()), SingleStepCallback);
});
}
Note that the callback that the recursive algorithm uses for single stepping is different than the callback for simply running the algorithm to conclusion.
Our stepper then releases the semaphore:
public override bool Step()
{
++Iterations;
bool isSolved = !(board.RemainingPegs == 1);
hopSemaphore.Release();
return isSolved;
}
The callback performs the hop, sets the solved flag, and waits until the semaphore is released again before returning to the recursion algorithm:
protected bool SingleStepCallback(Hop hop)
{
board.HopPeg(hop);
Solved = board.RemainingPegs == 1;
hopSemaphore.WaitOne();
return Solved;
}
An astute question is, why isn't this call:
board.HopPeg(hop);
marshaled onto the main thread? The reason is that the UI code that handles the DoHop and UndoHop events only updates the text boxes and list boxes when the algorithm is running, not when the algorithm is single stepping. The stepper UI code updates these controls separately on the main application thread. A further explanation of this logic will be revealed when we discuss the UI next.
Next, we'll look at the UI.

The game board is rendered by embedding the FlowSharp canvas, which is a four step process:
Bootstrap("modules.xml");
The minimum set of modules needed is described in the XML file:
<Modules>
<Module AssemblyName='Clifton.SemanticProcessorService.dll'/>
<Module AssemblyName='FlowSharpService.dll'/>
<Module AssemblyName='FlowSharpCanvasService.dll'/>
<Module AssemblyName='FlowSharpMouseControllerService.dll'/>
<Module AssemblyName='FlowSharpToolboxService.dll'/>
<Module AssemblyName='FlowSharpRestService.dll'/>
<Module AssemblyName='FlowSharpWebSocketService.dll'/>
</Modules>
Read more about the bootstrap process and FlowSharp's SOA:
This sets up the canvas:
protected void InitializeFlowSharp()
{
var canvasService = Program.ServiceManager.Get<IFlowSharpCanvasService>();
canvasService.CreateCanvas(pnlFlowSharp);
canvasService.ActiveController.Canvas.EndInit();
canvasService.ActiveController.Canvas.Invalidate();
var toolboxService = Program.ServiceManager.Get<IFlowSharpToolboxService>();
Panel pnlToolbox = new Panel();
pnlToolbox.Visible = false;
Controls.Add(pnlToolbox);
toolboxService.CreateToolbox(pnlToolbox);
toolboxService.InitializeToolbox();
var mouseController = Program.ServiceManager.Get<IFlowSharpMouseControllerService>();
mouseController.Initialize(canvasService.ActiveController);
}
protected void DrawBoard()
{
int cx = (pnlFlowSharp.Width - 50)/2;
int y = 50;
int n = 0;
Rectangle trect = new Rectangle(cx - NUM_ROWS * 50 + 65, y - 15, NUM_ROWS * 50 + 100, y + NUM_ROWS * 50 + 25);
WebSocketHelpers.DropShape("UpTriangle", "t", trect, Color.FromArgb(240, 230, 140));
NUM_ROWS.ForEach(row =>
{
row.ForEach(cell =>
{
string name = "c" + n;
Rectangle rect = new Rectangle(cx - 25 * row + 50 * cell, y + row * 50, 30, 30);
WebSocketHelpers.DropShape("Ellipse", name, rect, Color.White);
WebSocketHelpers.UpdateProperty(name, "Text", n.ToString());
++n;
});
}, 1);
}
Notice the funky integer ForEach extension method! Also notice that communication between the application and FlowSharp is done over a websocket channel. Why? Because typically FlowSharp is running as a completely separate application, rather than an embedded application, and I never implemented the interface methods for drawing shapes and setting shape properties. However, this does mean that when you run the demo for the first time, you'll probably see this:

 So just go ahead and click on Allow access. There isn't anything else nasty going on.
So just go ahead and click on Allow access. There isn't anything else nasty going on.
(ok, that's bizarre. The above image is Copyright 2004 by Melissa Clifton. No relation that I know of! Also, explicit permission to use that image has been given. Visit her website!)
Lastly, we draw the pegs:
protected void ShowPegs()
{
board.NumCells.ForEach(n => WebSocketHelpers.UpdateProperty("c" + n, "FillColor", board.GetPegColor(n).Name));
WebSocketHelpers.UpdateProperty("c" + startPosition, "FillColor", "White");
}

The game board fires these events, which the UI hooks:
board.DoHop += OnHop;
board.UndoHop += OnUndoHop;
When a hop is performed, the canvas is updated to reflect the change:
protected void OnHop(object sender, CellChangeEventArgs e)
{
if (ckShowUi.Checked)
{
UpdateUI(
e.Hop.FromCellIndex, e.Hop.HoppedCellIndex, e.Hop.ToCellIndex,
Color.White, Color.White, board.GetPegColor(e.Hop.ToCellIndex));
}
}
The checkbox being checked (no pun intended) is used to prevent the UI from updating. Certain starting positions (peg #2, 11, and 13) take a LOT of iterations (~32,000, ~24,000, ~24,000 respectively). You can sit around for several minutes (or longer depending on the delay you've set) waiting for the solution watching the circles blink, or you can uncheck the "UI" checkbox and the solution will be presented pretty much instantly.
Notice that when a hop is performed, the "from cell" and "hopped cell" are turned white, and the "to cell" gets the peg color of the new "to cell" peg color (that was sort of redundant to say it that way.)
Undoing a hop is the opposite:
protected void OnUndoHop(object sender, CellChangeEventArgs e)
{
if (ckShowUi.Checked)
{
UpdateUI(
e.Hop.FromCellIndex, e.Hop.HoppedCellIndex, e.Hop.ToCellIndex,
board.GetPegColor(e.Hop.FromCellIndex), board.GetPegColor(e.Hop.HoppedCellIndex), Color.White);
}
}
the "from" and "hopped" cells are restored to their current peg colors, and the "to" cell is emptied.
What is this? It's a bit of a kludge of updating the controls and injecting a user-controlled delay for each step when the algorithm is running.
protected void UpdateUI(int fromIdx, int hopIdx, int toIdx, Color fromColor, Color hoppedColor, Color toColor)
{
WebSocketHelpers.UpdateProperty("c" + fromIdx, "FillColor", fromColor.Name);
WebSocketHelpers.UpdateProperty("c" + hopIdx, "FillColor", hoppedColor.Name);
WebSocketHelpers.UpdateProperty("c" + toIdx, "FillColor", toColor.Name);
if (running)
{
lbSolution.DataSource = algorithm.UndoStack.Reverse().ToList();
tbIterations.Text = algorithm.Iterations.ToString("#,###,##0");
Application.DoEvents();
System.Threading.Thread.Sleep(tbIterateDelay.Text.to_i());
}
}
The code comments are most revealing, as there's a certain entanglement between single stepping and running the algorithm. And of course, we have to explicitly let the control updates (including the canvas) do their thing.
Changing the starting position updates the game board canvas and the internal start position field:
private void OnStartPositionChanged(object sender, EventArgs e)
{
startPosition = (int)nudStartPosition.Value;
ShowPegs();
}
A real no-brainer!
Regardless of which algorithm you choose, running the solver is the same:
private void btnRun_Click(object sender, EventArgs e)
{
singleStepping = false;
ShowPegs();
algorithm.Initialize(startPosition);
running = true;
solutionHops?.Clear();
lbSolution.DataSource = new List<Hop>();
algorithm.Run();
running = false;
if (algorithm.Solved)
{
solutionHops = algorithm.UndoStack.Reverse().ToList();
RestoreBoard();
solutionHops.Add(new Hop(-1, 0, 0));
lbSolution.DataSource = solutionHops;
tbIterations.Text = algorithm.Iterations.ToString("#,###,##0");
solutionStep = 0;
ckShowUi.Checked = true;
board.FillAllCells();
board.RemovePeg(startPosition);
}
else
{
MessageBox.Show("No Solution!", "Brain Teaser", MessageBoxButtons.OK, MessageBoxIcon.Exclamation);
}
}
One of the things that took a while to realize was that I needed to unwind the solution stack to restore the original board colors (along with the earlier-mentioned cloning of the Hop instance):
protected void RestoreBoard()
{
while (algorithm.UndoStack.Count > 0)
{
Hop hop = algorithm.UndoStack.Pop();
board.UndoHopPeg(hop);
Application.DoEvents();
}
}
Sure, I could have just reset the colors from the initial state of the cells, but this is a nice proof that undoing all the operations results in the initial game board setting. And I worked hard to figure out the issues with this!
While the algorithm is running, all the controls are disabled except the ability to change the delay for each step as it is processed.
protected void EnableUI(bool state)
{
(new Control[] { btnStart, btnSingleStep, nudStartPosition, lbSolution, cbAlgorithm, ckShowUi }).ForEach(ctrl => ctrl.Enabled = state);
}
When the user initiates single stepping, this code runs, again regardless of the algorithm:
private void btnSingleStep_Click(object sender, EventArgs e)
{
ckShowUi.Checked = true;
if (!singleStepping)
{
running = false;
ShowPegs();
algorithm.Initialize(startPosition);
algorithm.StartStepper();
}
bool next = algorithm.Step();
tbIterations.Text = algorithm.Iterations.ToString("#,###,##0");
if (next)
{
algorithm.PushHop();
lbSolution.DataSource = algorithm.UndoStack.Reverse().ToList();
}
singleStepping = next || (board.RemainingPegs > 1 && next);
}
The iteration counter and ListBox updates as the algorithm works on finding a solution, giving you a nice visual of the process. This PushHop method is sort of an eye-sore for me, as it is only used by the iterating algorithm. You'll also notice some other methods, in each algorithm, that don't do anything because they are not relevant for the specific algorithm implementation.
Lastly, once a solution is found (every starting position has a solution) you can click on a step in the ListBox or cursor up/down (once the ListBox is selected) and see the solution at your leisure, and memorize a couple to impress your friends!
protected void OnSolutionStepChanged(object sender, EventArgs e)
{
int newSolStep = lbSolution.SelectedIndex;
while (newSolStep > solutionStep)
{
board.HopPeg(solutionHops[solutionStep++]);
}
while (newSolStep < solutionStep)
{
board.UndoHopPeg(solutionHops[--solutionStep]);
}
}
You'll have to download and build the code to change the algorithm:
protected void OnShown(object sender, EventArgs e)
{
board = new Board(NUM_ROWS);
algorithm = new IterativeAlgorithm(board);
board.DoHop += OnHop;
board.UndoHop += OnUndoHop;
WebSocketHelpers.ClearCanvas();
DrawBoard();
ShowPegs();
}
 Just kidding! I overcame my laziness (this article has taken way too long, haha):
Just kidding! I overcame my laziness (this article has taken way too long, haha):

protected void OnSelectedIndexChanged(object sender, EventArgs e)
{
algorithm = new Algorithm[]
{
new IterativeAlgorithm(board),
new RecursiveYieldAlgorithm(board),
new RecursiveStepAndContinueAlgorithm(board)
}[cbAlgorithm.SelectedIndex];
}
Hmmm. Do you like this better:
protected void OnSelectedIndexChanged(object sender, EventArgs e)
{
algorithm = Activator.CreateInstance(new Type[]
{
typeof(IterativeAlgorithm),
typeof(RecursiveYieldAlgorithm),
typeof(RecursiveStepAndContinueAlgorithm)
}[cbAlgorithm.SelectedIndex], new object[] { board }) as Algorithm;
}
Didn't think so. I suppose you were expecting a switch statement? From me???
As usual, while the code took about 3 hours to write, the article took 3 times longer! Good grief.
On the other hand, I think one of the coolest things about what I've presented here are the three different algorithms: iteration, recursive yield, and recursive step-and-continue, and as usual, in writing the article, a lot of code cleanup occurred!
The source code can also be found on GitHub here.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 












