Classification using Logistic Regression in Visual Basic

• Download source code - 88.9 KB
• Download latest source code - https://github.com/chlohe/VBML

Introduction

Logistic regression is an exciting bit of statistics that allows us to find relationships in data when the dependent variable is categorical. On account of this, it has captivated the minds of many a statistician to such a degree that my school uses it to help them predict A-level grades.

In this article, we will discuss a simple binary (only outputs “yes” or “no”) implementation of logistic regression in Visual Basic and use it to make predictions based on data in spreadsheets.

Background

Super Important Terms

Hypothesis – How we predict something works (e.g., “I hypothesize that the relationship between height, age and weight is given by the function w = 5h + 2a + 1”).

Parameter Vector – The vector containing what are effectively the coefficients for your hypothesis (e.g., 5, 2 and 1 are contained in the parameter vector for the previous weight-height model). They are, for some reason, represented with the Greek letter θ.

Feature – A measurable property of a phenomenon being observed (e.g., height and age are the features in the previous weight-height model)

Likelihood – The probability of getting a certain dataset using a certain hypothesis given a certain parameter vector

Posterior Probability – The probability of getting a certain hypothesis with a certain parameter vector given a certain dataset

How Does One Go About Turning a Parameter Vector and Values into a Hypothesis?

With ease.

Using the weight predictor as an example, let 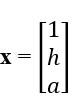and .

We want to get w = 5h + 2a + 1. Hmm.

If we multiplied each element in x by their corresponding element in θ, we’d get

h(x) = 1*1 + 5*h + 2*a

Put in a more abstract way, with and , our hypothesis is .

This can be done with a for-loop or, if you’re feeling extra sneaky, matrix multiplication (x^Tθ).

How Does One Go About Turning Hypotheses into Predictions?

Now that we have a hypothesis, we need to make predictions – we need to find some sort of function that maps h(x) to some value between 1 and 0 (“yes” and “no” respectively). It just so happens that a certain mathematician, Pierre François Verhulst by name, came up with exactly such a function while he was studying population growth: the standard logistic function (also called a “sigmoid” function because it looks like an “s”).

We simply pass in our hypothesis and get out a prediction. If the function is unsure, it’ll return a fraction: 0.9 means it’s pretty sure that it’s got a 1; 0.4 is a less sure 0.

Wait a Second, How Do We Get the Values for θ?

Assuming that we have example data to train with, we are now faced with an optimisation problem: to find values for θ that minimise the error in our predictions (thus optimising our model). The problem can be broken up into two parts:

Part 1: How Wrong Are We?

For each vector θ, we need to work out how wrong the model based upon the values is. The error metric we’re going to use is the negative log likelihood.

We define it thus:

The graphs for these cases are shown below:

Where the red line shows . We can see that the functions have asymptotes at x = 0 and x = 1 and that they strongly penalise wrong predictions with made high certainty (when y = 0 but we predicted something like 0.9). We can combine the expressions thus:

Where N is the number of examples in x, y_i is the i^th value in y and x_i is the i^th example in x.

Note that when y_i = 0, the first term in the sum reduces to 0; when y_i = 0, the second term reduces to 0. We take a log transform to make the function easier to handle – small numbers that might experience underflow become less small; multiplication becomes addition. A very good derivation can be found here: http://www.robots.ox.ac.uk/~az/lectures/ml/2011/lect4.pdf.

Part 2: How Can We Stop Being Wrong?

To stop being wrong, we have to minimise the errors we make. One of the most intuitive methods of doing this makes use of elementary calculus. The negative log likelihood function for logistic regression can be shown to be concave – that is that there exists a single global optimum.

We thus take partial derivatives for all θ, multiply them by a learning rate (step size) α and then subtract them from their respective original values: where f represents a certain feature. Looping over many times, this essentially moves us closer to the optimum – like a skateboarder rolling down a valley – where for all θ.

In the case of our logistic function, the derivative can be easily obtained from the chain rule:

We thus arrive at the following update function:

Where f is a feature, α is the learning rate and x_i [f] is the value of feature f in example x_i.

In summary, our algorithm takes the following form:

Repeat for all features:

If gradient is within reasonable threshold, then exit loop.

Optimising the Optimiser

We can see that convergence slows down as we approach the optimum. This is because the partial derivatives begin to near 0 and the step sizes become very small. We can counteract this by making the following tweaks to the algorithm:

• Record the squared partial derivatives for each feature in an array .
• Divide the learning rate for each feature by the square root of the sum of the last 10 partial derivatives.

This dynamically changes the learning rate as we approach convergence.

We can speed up convergence further by normalising all the features. We could also take a stochastic approach by updating the parameter vector after every training example we go over though this converges “less”.

Need Even More Speed?

Use a different algorithm but remember: inverting matrices is effort. Newton's method is pretty easy to do with a decent linear algebra library.

Using the Code

CSV data is loaded into using the Load() method. The data should have headings in the top row.

Load("path/to/my_file_name.csv")

Our logistic function and error cost function are implemented below:

Function LogisticFunction(x)
    'Compute the value of the logistic function given input x
    'a sigmoid function has an S shape and is given by 1/(e^(-t))
    'e = 2.71... (Euler's number)

    Return (1 / (1 + Math.Exp(-x)))

End Function

Function LogisticCost()

    Dim cost As Double

    'Loop through all the training examples
    For i = 0 To exampleCount - 1

        Dim exampleCost As Double

        If exampleOutputs(i) = 0 Then
            exampleCost = Math.Log(1 - LogisticFunction(Hypothesis(exampleInputs(i))))
        Else
            exampleCost = Math.Log(LogisticFunction(Hypothesis(exampleInputs(i))))
        End If

        cost += exampleCost

    Next

    'Take average
    cost *= -1 / exampleCount

    Return Math.Abs(cost)

End Function

And our optimisation algorithm is implemented here:

Sub Minimise()

    'Simple implementation of adagrad bc no way in hell 
    'am I implementing bfgs or anything that requires the hessan
    'gradient = X'(h(x) - y)

    Dim learningRate As New List(Of Double)
    Dim derivative As New List(Of Double)
    Dim pastGradientSquares As New List(Of List(Of Double))
    Dim sumOfPastGradientSquares As New List(Of Double)

    'Initialise all the variables
    For i = 0 To featureCount
        derivative.Add(1)
        learningRate.Add(0.01)
        sumOfPastGradientSquares.Add(0)
        pastGradientSquares.Add(New List(Of Double))
    Next

    lastCost = LogisticCost()
    deltaCost = 100

    'Do this until we converge (the derivative = 0ish)
    While (Math.Abs(deltaCost) > desiredDelta)

        Dim difference As New List(Of Double)
        Dim h As New List(Of Double)

        'Reset the derivative
        For i = 0 To thetas.Count
            derivative(i) = 0
        Next

        'Loop through the hypotheses and populate the list h

        For i = 0 To exampleCount - 1
            h.Add(LogisticFunction(Hypothesis(exampleInputs(i))))
        Next

        'Get the difference

        For i = 0 To exampleCount - 1
            difference.Add(h(i) - exampleOutputs(i))
        Next

        'Multiply by the features 

        For i = 0 To exampleCount - 1
            For j = 0 To featureCount - 1
                derivative(j) += difference(i) * exampleInputs(i)(j)

                'Update the list of previous squared derivatives
                pastGradientSquares(j).Add(Math.Pow(derivative(j), 2))

                'If we exceed 10 things, just remove the oldest entry 
                If pastGradientSquares(j).Count > 10 Then
                    pastGradientSquares(j).RemoveAt(0)
                End If

                'Update the sums
                sumOfPastGradientSquares(j) = Sum(pastGradientSquares(j))

            Next
        Next

        'Multiply by Learning Rate for this specific feature and get new thetas

        For i = 0 To featureCount - 1
            thetas(i) -= (learningRate(i) / _
            (Math.Sqrt(sumOfPastGradientSquares(i) + 0.00000001))) * derivative(i)
        Next

        Dim currentCost = LogisticCost()
        deltaCost = currentCost - lastCost

        'We need to look like we're doing something 
        'so here's something to keep users occupied
        Console.WriteLine("Training...  " + LogisticCost().ToString + _
                          " " + derivative(0).ToString) ' + " " + _
                          derivative(1).ToString + " " + derivative(2).ToString)

        lastCost = currentCost

    End While

End Sub

We can quickly get predictions like this:

Function Predict(x)

    Return LogisticFunction(Hypothesis(x))

End Function

And see how well our classifier is doing like this:

Sub Check()

    Dim correctlyClassified As Double = 0

    'Loop through results and see how many were classified correctly
    For i = 0 To exampleInputs.Count - 1

        Dim result As String
        If Predict(exampleInputs(i)) > 0.5 Then
            result = "Positive"
            If exampleOutputs(i) = 1 Then
                correctlyClassified += 1
            End If
        Else
            result = "Negative"
            If exampleOutputs(i) = 0 Then
                correctlyClassified += 1
            End If
        End If

        Dim trueClassification As String
        If exampleOutputs(i) = 1 Then
            trueClassification = "Positive"
        Else
            trueClassification = "Negative"
        End If

        Console.WriteLine(result + " and was actually " + trueClassification)

    Next

    Console.WriteLine("Correctly Classified " + _
       correctlyClassified.ToString + " out of " + exampleInputs.Count.ToString)

End Sub

Demo

The classifier was trained on made-up data to model some real-life situations. Using the below data, a model was built to predict car crashes based upon wheel drive, age of car and weather conditions.

The resulting predictions looked a bit like this:

Another dataset was used to predict whether pupils would pass their exams based upon the hours they spend studying, their previous performance and whether or not they’re in a relationship.

The resulting predictions were:

Other Things to Look Into

Regularization

Sometimes our models may over-fit the data. That's a bad thing because although it might be better at classifying the training set, it may become less suitable at making predictions with new data. Regularization allows us to stop it.

Multiclass Classification

Classifying things into more than just "Positive"s and "Negative"s. This can quite crudely be done by creating a classifier for each class, passing your input through all of them and then choosing the highest-scoring classification.

For instance, with three classes, cat, dog and table, an image of a cat might score 0.9 on the cat classifier, 0.4 on the dog classifier and 0.001 on the table classifier. We then select the classifier with the 0.9 score and return "it's a cat".

Source

• https://github.com/chlohe/VBML

History

• 19^th December, 2016: Initial version